LE TPE QUI PARLAIT DU NOMBRE D'OR ET DU TOURNESOL
Par Lucie Mayolle et Stella Mollicone
Par Lucie et Stella
Chez certaines plantes, les feuilles et les fleurs s’organisent selon des structures géométriques régulières, et l’étude de ces agencements s’appelle la phyllotaxie.
La manière dont ces structures apparaissent au cour de la croissance de la plante est intéressante d'un point de vue scientifique.
On peut les modéliser à l’aide des mathématiques et plus particulièrement grâce au nombre d’or.
Nous allons répondre à cette problématique grâce au tournesol qui est selon nous le meilleur exemple, en raison de la disposition particulière des spirales au cœur de sa fleur.
Tout d'abord nous allons introduire les bases mathématiques, pour ensuite nous intéresser aux plantes et au rapport qu'elles entretiennent avec ce nombre d'or.
Quelle est la place du nombre d'or chez certaines plantes?(et plus particulièrement chez le tournesol)
LES BASES MATHEMATIQUES
Le nombre d'or est un nombre aux propriétés mathématiques particulières.
Comme pi, c'est un nombre irrationnel, c'est-à-dire qu'il ne peut pas s'écrire sous forme de fraction.
Par exemple 1,5=3/2 , c'est un nombre rationnel.
Mais Pi est égal à 3,1415... on ne peut pas l'écrire sous forme de fraction.
La valeur approchée du nombre d'or est 1,61803398875
On le représente par la lettre Phi.
Dans notre perception de l'espace, il est associé à l'harmonie. Ses rapports sont appelés la Divine Proportion. Ils représentent la proportion idéale pour un objet, esthétiquement parlant.
On dit qu'on peut le retrouver dans plusieurs bâtiments et œuvres d'arts, par exmple la pyramide de Khéops et le Parthénon.
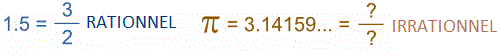

Lettre Phi
Au IIIe siècle avant JC , Euclide, un mathématicien de la Grèce Antique ,
donne la première définition du nombre d'or :
On prend un segment [ac] avec un point b appartenant à [ac].
On cherche à placer b tel que :

Mettons ce problème sous forme d'équation :

EUCLIDE




On a :
On pose :
On trouve x²-x-1=0 qui est un polynôme du second degré.

Il existe deux solutions à l'équation x²-x-1=0 : et qui est le nombre d'or.


=1/
Lorsqu'on décompose un objet en deux parties inégales, on dit que la proportion est divine, ou dorée, si le rapport entre la grande partie et la petite est le même que le rapport entre l'ensemble des 2 et la grande partie > soit le nombre d'or.
Le nombre d’or peut être défini en termes de lui-même et étendu indéfiniment.
Démonstration avec la fraction infinie :


On obtient une fraction qui ne se termine jamais !
Nous allons à présent vous présenter la suite de Fibonacci.
Il existe une relation très spéciale entre le nombre d’or et cette suite.
Tout d’abord, qui était Fibonacci ?

Fibonacci était un moine mathématicien italien de la fin du 12ème siècle et début 13ème siècle qui étudiait les suites continues. Il est connu pour avoir découvert cette suite et pour avoir aidé à répandre les chiffres arabes à travers l'Europe pour remplacer les chiffres romains. Son vrai nom était Leonardo Pisano, et il se surnommait lui-même Fibonacci.
FIBONACCI
En 1202 il se pencha sur le problème de la croissance des populations de lapins.
On réalise une étude en partant d’une paire de bébés lapin. On part avec un principe simple :
A leur deuxième mois ces 2 lapins sont capables de se reproduire, et chaque nouvelle portée de lapins est une paire composée d'un mâle et une femelle. Les lapins ne meurent jamais et une paire fait une nouvelle paire de lapin chaque mois à partir de son 2ème mois.
On obtient donc le schéma ci-dessous :

Le but est de compter le nombre total de paires de lapins à chaque nouvelle génération.
Au deuxième mois la première paire est adulte ; puis elle engendre une deuxième paire, qui ensuite va en faire une autre…. En comptant le nombre de paires lapins chaque mois, on obtient : 1,1,2,3,5,8…
Si on continue cette logique on obtient la suite de Fibonacci.
Qu’est-ce qu’une suite ?
C'est une suite de nombres que l’on obtient en ajoutant une constante au précédent. Elle est définie par un premier nombre et par une règle.
La suite de Fibonacci est une suite de nombres entiers, où le nombre suivant est la somme des 2 précédents.
La règle de la suite est xn =xn-1 + xn-2

Par exemple la 10ème valeur est la somme de la 8ème et 9ème valeur : 21+34=55
Quel est donc le rapport entre la suite de Fibonacci et le nombre d’or ?
Le rapport entre 2 nombres consécutifs de la suite de Fibonacci donne un nombre très proche du nombre d'or : (exemple : 610 /377=1,618037...)
Et plus ces nombres sont grands, plus on se rapproche du nombre d'or.
Propriétés intéressantes de la suite de Fiboancci :
-
Pour toute valeur n de la suite de fibonacci associée à son nombre Xn, toutes les n valeurs on obtient un multiple de Xn.
Exemples :
- Regardons le 3ème nombre de la suite, il s’agit du chiffre 2. Tous les 3 nombres sont des multiples de 2.
- Quand on prend le 6ème nombre de la suite on tombe sur un 8 ; tous les 6 nombres de la suite on tombe sur un multiple de 8.
-
On a aussi : 1 / φ=φ - 1
Passons à l’angle d’or.
Qu’est-ce que l’angle d’or ?
Parlons de rotations sur un cercle.
Si 1 équivaut à un tour complet, soit 360°, alors l’équivalent de 0,61803...tour est 222,4922 degrés, ou environ 222,5°.
On prend l'angle opposé, qui mesure 137,5°. On l'apelle l’angle d’or.

LES PLANTES ET LEUR RELATION AVEC LE NOMBRE D'OR
A présent il est temps de vous parler des plantes.
Il existe énormément de structures différentes chez les plantes.
Sur la tige plusieurs feuilles peuvent être attachées en un même point, ce point s'appelle le nœud.
On trouve trois grands types d’organisation des feuilles sur une tige :
- le cas opposé où deux feuilles sont sur un même nœud
- le cas spiralé où les feuilles sont seules et décalées
- le cas verticillé où il y a au moins 3 feuilles par nœud.
Chez certaines plantes, on peut voir que les feuilles sont disposées en spirales avec un certain angle appelé angle de divergence.
On peut se demander pourquoi il s'agit de cet angle-là, et s’il apporte un quelconque bénéfice à la plante. Il existe une théorie selon laquelle les feuilles sont décalées par rapport à celles du dessus pour mieux optimiser leur exposition au soleil.
Cependant la disposition des feuilles est très différente selon les espèces, la nature s'adapte en fonction des cas.
De plus les feuilles peuvent s'orienter dans l'espace (ex : si on met une plante devant une fenêtre et qu'on l'oriente vers l'intérieur, les feuilles, après quelques semaines, seront à nouveau braquées vers la lumière.)
Nous allons voir quelles sont ces dispositions, mais surtout qu’elles ne concernent pas uniquement les feuilles mais aussi d'autres éléments botaniques tels que les écailles de pomme de pin ou les fleurs de tournesol.
Ces éléments sont disposés de façon à économiser l'espace, et nous verrons comment.
Passons au cas du tournesol.


Premièrement qu'est-ce qu'un tournesol ?
A première vue le tournesol est une grosse fleur, mais il s'agit en fait d'une inflorescence :
elle est composée de beaucoup de petites fleurs avec de tout petits pétales, qui donneront des graines ; ce sont les fleurons.
Il y a 2 types de fleurons : ceux qui sont au centre sont fertiles et hermaphrodites, et semblent former le cœur de la grosse fleur.
Aux extrémités les fleurons ont de très longs pétales jaunes qui semblent être les pétales de la grosse fleur. Ces fleurs là sont stériles et seulement décoratives.
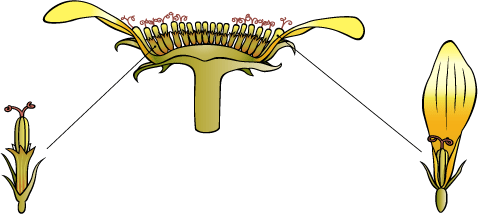

Ces deux images montrent bien que les fleurons, (et même ceux qui semblent être les "pétales" du tournesol) sont des fleurs.
Les nouveaux fleurons apparaissent au centre, appelé méristème.
Les plus vieux sont situés à l’extérieur.
L'ensemble qui contient toutes ces fleurs s'appelle le capitule.
Le fait que les fleurons soient groupés en un ensemble permet aux petites fleurs d'être mieux vues par les insectes et favorise la pollinisation.
On remarque une configuration intéressante : les fleurons sont arrangés en spirale ! Elles s'appellent les parastiches.

Ces spirales apparaissent naturellement car chaque nouvelle cellule apparaît décalée de la précédente par rapport à un certain angle, l'angle de divergence que nous allons étudier ci-dessous.
Un peu d'histoire :
En 1837 le cristallographe Auguste Bravais a observé un détail crucial :
il traça les droites joignant les fleurons au centre de la fleur et mesura les angles qui séparaient deux fleurons successifs dans le temps : ils mesurent tous 137,5 degrés, soit l’angle d’or..


Sur la ligne, l'angle qui sépare 2 fleurons successifs par rapport au centre mesure 137,5°
On voit ici que l’angle d’or a un lien étroit avec les fleurons du tournesol.
C’est également cet angle qui, dans le cas spiralé, est présent entre chaque feuille consécutive.

On a ici une plante du genre spiralé :
137,5° séparent deux feuilles consécutives.
Cette disposition pourrait permettre aux feuilles de la plante d’avoir un apport de soleil optimal, car elles ne se feraient pas d’ombre entre elles.
Revenons au cas de la fleur de tournesol :
Nous avons dit plus haut qu'entre chaque nouveau fleuron qui apparaît, il y a un angle précis.
Mais nous pouvons trouver un rapport direct entre les fleurons et le nombre d'or.
Premièrement, nous pouvons poser le problème ainsi :
il y a un certain nombre de tours entre chaque nouveau fleuron. ( le chiffre 1 équivaut à un tour complet, soit 360°)
Quel nombre permet donc d'obtenir la structure présentant le moins d’espace entre chaque fleuron ?
Nous allons répondre à cette question à l’aide d’une animation, qui modélise la structure des spirales en fonction de ce nombre.
L'objectif est donc d'avoir le moins d'espace possible entre les fleurons du tournesol.
Utiliser n'importe quel nombre compris entre 0 et 1 , tel que 0,9 ou 0,619 donnera un motif d'alignement qui comportera des lacunes.
Essayez par vous-même cette animation en cliquant ICI
Le nombre qui permet d'avoir une optimisation parfaite de l'espace est le nombre d'or, encore une fois.
Quand un fleuron apparaît tous les 0,618 tour, le tournesol ne comporte pas de trous.
C'est une démonstration directe de la présence, et de l'utilité du nombre d’or pour le tournesol, car cet arrangement est compact, et permet d’obtenir une structure ronde sans espace.



A présent nous allons montrer la présence de la suite de Fibonacci dans le tournesol.
Les spirales formées par les fleurons sont orientées dans 2 sens différents : horaire et antihoraire.
Si on compte le nombre de spirales dans chaque sens, on obtient un résultat étonnant :
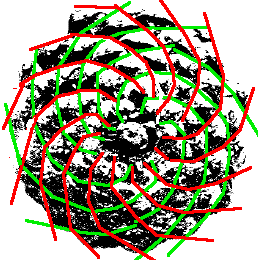
le nombre de spirales dans le sens horaire et antihoraire sont 2 nombres consécutifs de la suite de Fibonacci ! ( on obient par exemple 13 et 21 ; 34 et 55…)

34 spirales vers la droite, et 55 vers la gauche !
Certains tournesols ont jusqu’à 233 spirales !
D’autres plantes présentent aussi cette particularité : la pomme de pin, l’ananas, la marguerite ou encore le chou !

Cette pomme de pin comporte
13 spirales vers la gauche
et 8 vers la droite
sur ce chou romanesco, on compte 21 spirales vers la droite et 13 vers la gauche

21 et 34 chez cette marguerite

13 et 21 pour l'ananas
Ces spirales sont un très bon arrangement pour ces végétaux, qui leur permettent de disposer leur écailles/fleurs en économisant le plus d’espace possible.
POUR CONCLURE :
Au sein de la fleur de tournesol, on retrouve dans la disposition des fleurons le nombre d’or, l’angle d’or ainsi que la suite de Fibonacci.
Il y a donc une omniprésence du nombre d'or chez le tournesol, ainsi que chez certains autres paramètres végétal comme les feuilles et les écailles des pommes de pin.
Le nombre d’or occupe une place importante car il permet d’optimiser au maximum l’espace entre les fleurons et les écailles.
Nous connaissons la raison de cette disposition particulière chez le tournesol.
Cependant les autres espèces végétales, voire la nature-même, sont-elles aussi régies par les mathématiques ?